The Standard Model of particle physics is remarkably successful in describing the observed fundamental particles and their interactions at the level of precision we have been able to probe thus far in experiments. Despite this, there are several reasons to expect that it is only the low-energy (long-distance) description of a more fundamental theory. The Standard Model fails to explain certain observed experimental phenomena such as the matter-antimatter imbalance, dark matter and dark energy, and neutrino masses. It also leaves important theoretical questions unanswered, such as the origin of the particle masses and mixing parameters. Thus the foremost goal of the experimental high-energy physics program is to search for direct and indirect signs of new particles and forces.

Many experiments aim to search for quantum-mechanical effects of new particles that give rise to tiny deviations from Standard-Model expectations. Maximizing the new-physics discovery potential of these high-precision experiments requires reliable and equally precise theoretical predictions. In almost all cases, the precision of these tests are limited by our knowledge of the effects of the strong interaction (QCD) on weak-interaction processes. Numerical lattice-QCD simulations provide the only method for calculating the needed hadronic matrix elements and parameters of the QCD Lagrangian with controlled uncertainties that are systematically improvable. The objective of USQCD is to bring the lattice-QCD errors down to, or below, the experimental ones.

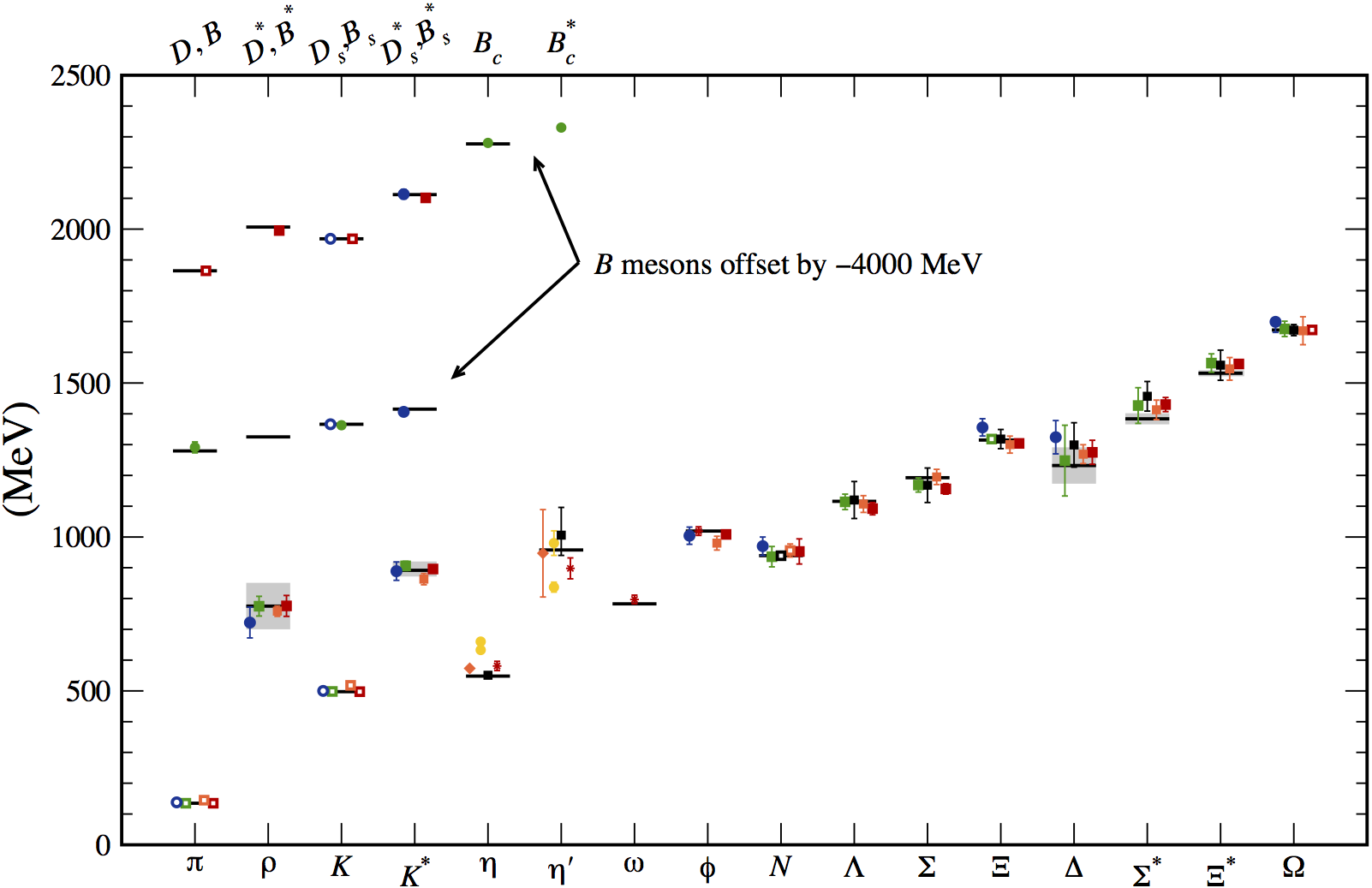
Compilation of lattice-QCD calculations of meson and baryon masses (update of Kronfeld 2012).

Over the past decade, increased computing power and better algorithms have led to substantial progress in the lattice-QCD computations of quantities needed to interpret experimental results in the areas of particle physics, nuclear physics, and even astrophysics. It is now standard in lattice-QCD simulations to include the full effects of vacuum polarization due to light (up, down and strange) quarks, and to simulate with pion masses close to the value in Nature. Lattice-QCD calculations successfully reproduce the experimentally-measured low-lying hadron spectrum, as shown in the figure at right. Lattice QCD provides the most precise determination of the strong coupling constant, α_s, and competitive determinations of the charm-and bottom-quark masses. Further, lattice-QCD calculations correctly predicted the mass of the B_c meson, the leptonic decay constants f_D and f_Ds, and the D → Klν semileptonic form factor before the availability of precise experimental measurements. These successful predictions and postdictions validate the methods of numerical lattice QCD, and demonstrate that reliable results can be obtained with controlled uncertainties.

Lattice-QCD calculations of the D- and D_s-meson decay constants. (From the Particle Data Group 2015.)

Lattice QCD has matured into a precision tool for quark-flavor physics. Results with fully controlled errors are available for nearly twenty matrix elements. By contrast, in 2007, only the ratio of kaon-to-pion decay constants, f_K/f_π, was fully controlled. The figure at left shows a recent compilation of lattice-QCD results for the D- and D_s-meson decay constants. There are now several calculations with controlled uncertainties using different lattice quark and gluon actions, which provide independent confirmation. The most precise calculations are from USQCD with errors of 0.6% and 0.5% on f_D and f_Ds, respectively, use a highly-improved charm-quark lattice action and include physical-mass pions. In the corresponding determinations of the Cabibbo-Kobayashi-Maskawa (CKM) quark-mixing matrix elements |V_cd| and |V_cs|, the lattice-QCD errors are now below the experimental errors.

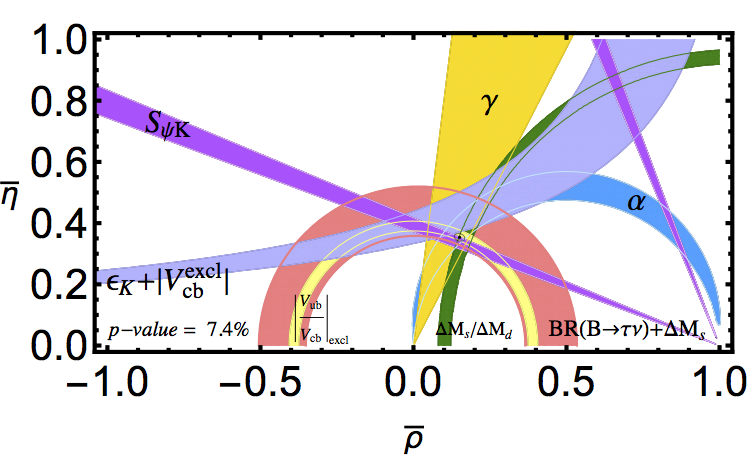
Constraints on the Cabibbo-Kobayashi-Maskawa quark-mixing matrix. Lattice-QCD calculations are essential to obtain constraints from neutral kaon mixing (lilac band) and neutral B_d- and B_s-meson mixing (green band), and also enable determinations of the CKM matrix elements |V_ub|/|V_cb| (bright yellow band). Recent lattice results have significantly tightened the constraints and increased the tension between them.

Recently, members of USQCD have produced new lattice-QCD results for the B → pi and B → K semileptonic form factors, the B → Dlν form factor at nonzero recoil, the ratio of Λ_b → Λ_clν/Λ_b → plν form factors, and the neutral B_d- and B_s-meson mixing matrix elements. These calculations led to significant improvements in the determinations of the Cabibbo-Kobayashi-Maskawa (CKM) quark-mixing matrix elements |V_ub|, |V_cb|, |V_td|, and |V_ts|. The figure at right shows constraints on the CKM matrix using the latest lattice-QCD inputs. In this plot, new-physics effects would show up as inconsistent constraints on the apex (ρ ,η) of the unitarity triangle. These recent lattice-QCD calculations substantially tightened several of the constraints and reduced the allowed Standard-Model parameter space. They also confirmed and/or revealed several tensions with the Standard Model of about 2 standard deviations in the quark-flavor sector.

USQCD is devoting considerable human effort and computing resources to meet the theory needs of current and upcoming high-energy physics experiments. Petascale computing is enabling better simulations with physical-mass pions, very fine lattice spacings, very large volumes, and dynamical charm quarks, all of which will lead to increase precision on present calculations. The precision on simple quantities is approaching the level where strong-isospin breaking and electromagnetic corrections are becoming relevant. Simulating with different up- and down-quark masses straightforward. Methods for are being developed to include electromagnetism in lattice simulations, and lattice QCD can already reproduce simple quantities such as the neutron-proton mass difference. USQCD is also targeting more challenging quantities needed by current and future experiments. Recently members of USQCD achieved the first complete QCD calculations of the mass difference between kaon eigenstates, which is a long-distance amplitude, and of the matrix elements for K → ππ decays, which has multiple hadrons in the final state. They also presented the first proof-of-principle demonstration of a method to calculate the light-by-light contribution to the muon anomalous magnetic moment (g−2). Continued efforts in developing new theoretical methods and better algorithms are ongoing. In the coming decade, anticipated progress in lattice-QCD calculations plus new experimental measurements will continue to increase the precision on Standard-Model parameters and sharpen tests of the Standard Model, hopefully revealing definitive evidence of physics beyond.